

Volumenberechnung beliebiger Körper mit Integralen ( Gerd Lamprecht) |


 ; Mantelfläche:
; Mantelfläche:
 denn
denn 


 sondern mit f(x)² und
sondern mit f(x)² und 

 *
* *EllipticE2
*EllipticE2
 sondern
sondern 

| 1 Paraboloid | |||
| 2 exponentiel | M= | ||
| 3 hyperbolischer Trichter (k=0.05) | 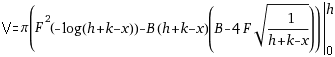 | M in Arbeit...; | |
| 4 = (2+3)/2 | (2+3)/2 | in Arbeit... | in Arbeit... |
| 5 Kegelstumpf (linear) | |||
| 6 halber Hyperboloid |  |
 , a=x1>=0, b=x2>x1
, a=x1>=0, b=x2>x1


