↑ ↓
genz
(1=gut)
↑ ↓



320 Berechnungswege für die Kreiszahl Pi (A000796 = 3.14159... aus Kreiszahl Pi ) |
|
Index ↑ ↓ |
Formel in Python (mpmath)↑ ↓ | Mathematica (Wolfram Doku)↑ ↓ | Algorithmus ↑ ↓ |
Konver genz (1=gut) ↑ ↓ | Herkunft ↑ ↓ | Datum ↑ ↓ |
|---|---|---|---|---|---|---|
| 001 | +pi | Pi | Konstante (intern) | ? | Programmiersprache | - |
| 002 | 180*degree | Degree*180 | Konstante (intern) | ? | Programmiersprache | - |
| 003 | atan(1)*4 | ArcTan[1]*4 | Trigonom.: atan | ? | ||
| 004 | acot(3)*8+acot(7)*4 | ArcCot[3]*8 + ArcCot[7]*4 | Trigonom.: Machin-like | ? | Hutton's or Vega's | |
| 005 | acot(49)*48+128*acot(57)-20*acot(239)+48*acot(110443) | ArcCot[49]*48+128*ArcCot[57]-20*ArcCot[239]+48 ArcCot[110443] | Trigonom.: Machin-like | ? | Kikuo Takano | 1982 |
| 006 | chop(2*j*log((1-j)/(1+j))) | Log[(1-I)/(1+I)]*2*I | Elementare Funktion komplex | ? | ||
| 007 | chop(-2j*asinh(1j)) | ArcSinh[I]*(-2)*I | Trigonom.: asinh komplex | ? | ||
| 008 | chop(ci(-inf)/1j) | CosIntegral[-Infinity]/I | Höhere Funkt.: CosIntegral | ? | ||
| 009 | gamma(0.5)**2 | Gamma[1/2]^2 | Höhere Funkt.: Gamma | ? | ||
| 010 | beta(0.5,0.5) | Höhere Funkt.: Beta | ? | |||
| 011 | (2/diff(erf, 0))**2 | (2/Erf'[0])^2 | Höhere Funkt.: Erf' | ? | ||
| 012 | findroot(sin, 3) | FindRoot[Sin[x], {x, 3}] | Nullstellensuche: sin | ? | Solve[Sin[x] == 0 && 3 < x < 4, x] | |
| 013 | acos(0)*2 | ArcCos[0]*2 | Trigonom.: acos | ? | findroot(cos, 1)*2 | |
| 014 | chop(-2j*lambertw(-ellipk(0))) | LambertW[EllipticK[0]*(-1)]*(-2)*I | Höhere Funkt.: LambertW, K | ? | ||
| 015 | besseljzero(0.5,1) | BesselJZero[1/2,1] | Höhere Funkt.: BesselJZero | ? | ||
| 016 | sqrt(3)*3/2/hyp2f1((-1,3),(1,3),1,1) | Sqrt[3]*3/2/Hypergeometric2F1[-1/3, 1/3, 1, 1] | Hypergeom. Funk. 2F1 | ? | ||
| 017 | 8/(hyp2f1(0.5,0.5,1,0.5)*gamma(0.75)/gamma(1.25))**2 | (Hypergeometric2F1[1/2,1/2,1,1/2]*Gamma[3/4]/Gamma[5/4])^(-2)*8 | Hypergeom. Funk. 2F1 | ? | ||
| 018 | 4*(hyp1f2(1,1.5,1,1) / struvel(-0.5, 2))**2 | (HypergeometricPFQ[{1},{3/2,1},1]/StruveL[-1/2,2])^2*4 | Hypergeom. Funk. 1F2 | ? | ||
| 019 | 1/meijerg([[],[]], [[0],[0.5]], 0)**2 | MeijerG[{{},{}},{{0},{1/2}},0]^(-2) | Hypergeom. Funk. MeijerG | ? | ||
| 020 | (meijerg([[],[2]], [[1,1.5],[]], 1, 0.5) / erfc(1))**2 | (MeijerG[{{},{2}},{{1,3/2},{}},1,1/2]/Erfc[1])^2 | Hypergeom. Funk. MeijerG | ? | ||
| 021 | (1-e)/meijerg([[1],[0.5]], [[1],[0.5,0]], 1) | MeijerG[{{1},{1/2}},{{1},{1/2,0}},1]^(-1)*(1-E) | Hypergeom. Funk. MeijerG | ? | ||
| 022 | sqrt(psi(1,0.25)-8*catalan) | (PolyGamma[1,1/4]-8*Catalan)^(1/2) | Höhere Funkt.: PolyGamma | ? | ||
| 023 | elliprc(1,2)*4 | Höhere Funkt.: | ? | |||
| 024 | elliprg(0,1,1)*4 | Höhere Funkt.: | ? | |||
| 025 | ellipk(0.75)*agm(1,0.5)*2 | EllipticK[3/4]*ArithmeticGeometricMean[1,1/2]*2 | Höhere Funkt.: EllipticK, AGM | ? | ||
| 026 | cbrt(gamma(0.25)**4*agm(1,sqrt(2))**2/8) | CubeRoot[Gamma[1/4]^4*ArithmeticGeometricMean[1,Sqrt[2]]^2/8] | Höhere Funkt.: Gamma, AGM | ? | ||
| 027 | sqrt(6*zeta(2)) | Sqrt[6*Zeta[2]] | Höhere Funkt.: Zeta | ? | ||
| 028 | sqrt(6*(zeta(2,3)+5./4)) | Sqrt[6*(Zeta[2,3]+5/4)] | Höhere Funkt.: Zeta | ? | ||
| 029 | sqrt(zeta(2,(3,4))+8*catalan) | Höhere Funkt.: Zeta | ? | |||
| 030 | exp(-2*zeta(0,1,1))/2 | Höhere Funkt.: Zeta | ? | |||
| 031 | sqrt(12*altzeta(2)) | Sqrt[DirichletEta[2]*12] | Höhere Funkt.: DirichletEta | ? | ||
| 032 | dirichlet(1,[0,1,0,-1])*4 | Höhere Funkt.: | ? | |||
| 033 | catalan*2/dirichlet(-1,[0,1,0,-1],1) | Höhere Funkt.: | ? | |||
| 034 | exp(-dirichlet(0,[0,1,0,-1],1))*gamma(0.25)**2/(2*sqrt(2)) | Höhere Funkt.: | ? | |||
| 035 | sqrt(7*zeta(3)/(4*diff(lerchphi, (-1,-2,1),(0,1,0)))) | Höhere Funkt.: | ? | |||
| 036 | sqrt(-12*polylog(2,-1)) | Sqrt[PolyLog[2,-1]*(-12)] | Höhere Funkt.: PolyLog | ? | ||
| 037 | sqrt(6*log(2)**2+12*polylog(2,0.5)) | Sqrt[Log[2]^2*6+PolyLog[2,1/2]*12] | Höhere Funkt.: PolyLog | ? | ||
| 038 | chop(root(-81j*(polylog(3,root(1,3,1))+4*zeta(3)/9)/2,3)) | Höhere Funkt.: PolyLog, Zeta | ? | |||
| 039 | clsin(1,1)*2+1 | Höhere Funkt.: | ? | |||
| 040 | (3+sqrt(3)*sqrt(1+8*clcos(2,1)))/2 | Höhere Funkt.: | ? | |||
| 041 | root(2,6)*sqrt(e)/(glaisher**6*barnesg(0.5)**4) | ((2^(1/24)*E^(1/8))/(Glaisher^(3/2)*BarnesG[1/2]))^4 | Höhere Funkt.: | ? | ||
| 042 | nsum(lambda k:(-1)**k/(2*k+1),[0,inf])*4 | Sum[(-1)^k/(2*k+1),{k,0,Infinity}]*4 | Reihe: | ? | Gottfried Wilhelm Leibniz | 1676 |
| 043 | nsum(lambda k:(3**k-1)/4**k*zeta(k+1),[1,inf]) | Sum[(3^k-1)/4^k*Zeta[k+1],{k,1,Infinity}] | Reihe: Zeta | ? | ||
| 044 | nsum(lambda k:8/(2*k-1)**2,[1,inf])**0.5 | Sqrt[Sum[8/(2*k-1)^2,{k,1,Infinity}]] | Reihe: | ? | ||
| 045 | nsum(lambda k:2*fac(k)/fac2(2*k+1),[0,inf]) | Sum[2*k!/Factorial2[2*k+1],{k,0,Infinity}] | Reihe: Factorial2 | ? | Ajima Naonobu | 1795 |
| 046 | nsum(lambda k:fac(k)**2/fac(2*k+1),[0,inf])*3*sqrt(3)/2 | Sum[k!^2/(2*k + 1)!, {k, 0, Infinity}]*(3*Sqrt[3]/2) | Reihe: | ? | ||
| 047 | nsum(lambda k:fac(k)**2/(phi**(2*k+1)*fac(2*k+1)),[0,inf])*(5*sqrt(phi+2))/2 | ((Sqrt[GoldenRatio+2]/2)*5)*Sum[k!^2/(GoldenRatio^(2*k+1) (2*k+1)!),{k,0,Infinity}] | Reihe: | ? | ||
| 048 | nsum(lambda k:(4/(8*k+1)-2/(8*k+4)-1/(8*k+5)-1/(8*k+6))/16**k,[0,inf]) | Sum[(4/(8*k+1)-2/(8*k+4)-1/(8*k+5)-1/(8*k+6))/16^k, {k,0,Infinity}] | Reihe: BBP 16 | ? | Jonathan & Peter Borwein | 1988 |
| 049 | 2/nsum(lambda k:(-1)**k*(4*k+1)*(fac2(2*k-1)/fac2(2*k))**3,[0,inf]) | 2/Sum[(-1)^k*(4*k + 1)*(Factorial2[2*k - 1]/Factorial2[2*k])^3, {k, 0,Infinity}] | Reihe: Kehrwert | ? | ||
| 050 | 1/nsum(lambda k:binomial(2*k,k)**3*(42*k+5)/2**(12*k+4),[0,inf]) | 1/Sum[Binomial[2*k,k]^3*(42*k+5)/2^(12*k+4),{k,0,Infinity}] | Reihe: Kehrwert | ? | Srinivasa Ramanujan Binomial[2*k, k] = (2*k)!/(k!)^2 | |
| 051 | 4/nsum(lambda k:(-1)**k*(1123+21460*k)*fac2(2*k-1)*fac2(4*k-1)/ (882**(2*k+1)*32**k *fac(k)**3),[0,inf]) | 4/Sum[(-1)^k*(1123+21460k)*Factorial2[2*k-1]*Factorial2[4*k-1]/(882^(2*k+1) 32^k k!^3), {k,0,Infinity}] | Reihe: Kehrwert | ? | ||
| 052 | 9801/sqrt(8)/nsum(lambda k:fac(4*k)*(1103+26390*k)/ (fac(k)**4*396**(4*k)), [0,inf]) | 9801/Sqrt[8]/Sum[(4*k)! (1103+26390*k)/(k!^4*396^(4*k)),{k,0,Infinity}] | Reihe: Kehrwert | ? | Srinivasa Ramanujan 1/Pi; vergl. 267 | 1914 |
| 053 | 4/nsum(lambda k:(6*k+1)*rf(0.5,k)**3/(4**k*fac(k)**3),[0,inf]) | 4/Sum[(6*k + 1)*Pochhammer[1/2, k]^3/(4^k*(k!)^3), {k, 0, Infinity}] | Reihe: Kehrwert | ? | ||
| 054 | (ln(8)+sqrt(48*nsum(lambda m,n:(-1)**(m+n)/(m**2+n**2),[1,inf],[1,inf])+9*log(2)**2))/2 | (Log[8]+Sqrt[48*Sum[(-1)^(m+n)/(m^2+n^2),{m,1,Infinity},{n,1,Infinity}]+9*Log[2]^2])/2 | Reihe: | ? | ||
| 055 | -nsum(lambda x,y:(-1)**(x+y)/(x**2+y**2),[-inf,inf],[-inf,inf],ignore=True)/ln2 | Sqrt[Sum[(-1)^(2 x)/(x^2*2), {x, 1, Infinity}]*12] | Reihe: | ? | ||
| 056 | nsum(lambda k:sin(k)/k,[1,inf])*2+1 | Sum[Sin[k]/k,{k,1,Infinity}]*2+1 | Reihe: | ? | ||
| 057 | quad(lambda x:2/(x**2+1),[0,inf]) | Integrate[1/(x^2+1),{x,0,Infinity}]*2 | Integral: | ? | ||
| 058 | quad(lambda x:exp(-x**2),[-inf,inf])**2 | Integrate[Exp[-x^2],{x,-Infinity,Infinity}]^2 | Integral: | ? | ||
| 059 | quad(lambda x:sqrt(1-x**2),[-1,1])*2 | Integrate[Sqrt[1-x^2],{x,-1,1}]*2 | Integral: | ? | ||
| 060 | chop(quad(lambda z:1/(2j*z),[1,j,-1,-j,1])) | Integrate[1/(2*I*z),{z,1,I,-1,-I,1}] | Integral: | ? | ||
| 061 | (log(2+sqrt(3))*4-quad(lambda x,y:1/sqrt(1+x**2+y**2),[-1,1],[-1,1]))*3/2 | (3*(4*Log[2+Sqrt[3]]-Integrate[1/Sqrt[1+x^2+y^2],{x,-1,1},{y,-1,1}]))/2 | Integral: | ? | ||
| 062 | sqrt(8*quad(lambda x,y:1/(1-(x*y)**2),[0,1],[0,1])) | Sqrt[8*Integrate[1/(1-(x*y)^2),{x,0,1},{y,0,1}]] | Integral: | ? | ||
| 063 | sqrt(6*quad(lambda x,y:1/(1-x*y),[0,1],[0,1])) | Sqrt[6*Integrate[1/(1-x*y),{x,0,1},{y,0,1}]] | Integral: | ? | ||
| 064 | sqrt(6*quad(lambda x:x/expm1(x),[0,inf])) | Sqrt[6*Integrate[x/(Exp[x]-1),{x,0,Infinity}]] | Integral: | ? | ||
| 065 | quad(lambda x:(16*x-16)/(x**4-2*x**3+4*x-4),[0,1]) | Integrate[(16*x-16)/(x^4-2*x^3+4*x-4),{x,0,1}] | Integral: | ? | ||
| 066 | quad(lambda x:sqrt(x-x**2),[0,0.25])*24+3*sqrt(3)/4 | Integrate[Sqrt[x-x^2],{x,0,0.25}]*24+3*Sqrt[3]/4 | Integral: | ? | ||
| 067 | mpf(22)/7-quad(lambda x:x**4*(1-x)**4/(1+x**2),[0,1]) | Integrate[x^4*(1-x)^4/(1+x^2),{x,0,1}]*(-1)+22/7 | Integral: | ? | ||
| 068 | mpf(355)/113-quad(lambda x:x**8*(1-x)**8*(25+816*x**2)/(1+x**2),[0,1]) /3164 | Integrate[x^8*(1-x)^8*(25+816*x^2)/(1+x^2),{x,0,1}]/(-3164)+355/113 | Integral: | ? | ||
| 069 | quadosc(lambda x:sin(x)/x,[0,inf],omega=1)*2 | Integrate[Sin[x]/x, {x, 0, Infinity}]*2 | Integral: | ? | ||
| 070 | quadosc(lambda x:sin(x)**6/x**6,[0,inf],omega=1)*40/11 | Integrate[Sin[x]^6/x^6, {x, 0, Infinity}]*40/11 | Integral: | ? | ||
| 071 | quadosc(lambda x:cos(x)/(1+x**2),[-inf,inf],omega=1)*e | Integrate[Cos[x]/(1 + x^2), {x, -Infinity, Infinity}]*E | Integral: | ? | ||
| 072 | quadosc(lambda x:cos(x**2),[0,inf],zeros=lambda n:sqrt(n))**2*8 | Integrate[Cos[x^2], {x, 0, Infinity}]^2*8 | Integral: | ? | ||
| 073 | quadosc(lambda x:sin(exp(x)),[1,inf],zeros=ln)*2+2*si(e) | Integral: | ? | |||
| 074 | exp(2*quad(loggamma,[0,1]))/2 | Exp[2*Integrate[LogGamma[x], {x, 0, 1}]]/2 | Integral: | ? | ||
| 075 | (exp(1+euler/2)/nprod(lambda n:(1+1/n)**n*exp(1/(2*n)-1),[1,inf]))**2/2 | Produkt | ? | |||
| 076 | nprod(lambda k:(1+2/k)**((-1)**(k+1)*k),[1,inf])*2/e | Produkt: | ? | |||
| 077 | limit(lambda k:16**k/(k*binomial(2*k,k)**2),inf) | Limit[16^k/(Binomial[2 k, k]^2*k), k -> Infinity] | Grenzwert: Bruch ganze Zahlen | ? | ||
| 078 | limit(lambda x:4*x*hyp1f2(0.5,1.5,1.5,-x**2),inf) | Grenzwert | ? | |||
| 079 | limit(lambda k:2**(4*k+1)*fac(k)**4/(2*k+1)/fac(2*k)**2,inf) | Grenzwert | ? | |||
| 080 | limit(lambda k:fac(k)/(sqrt(k)*(k/e)**k),inf)**2/2 | Grenzwert | ? | |||
| 081 | limit(lambda k:(-(-1)**k*bernoulli(2*k)*2**(2*k-1)/fac(2*k))**(-1/(2*k)),inf) | Grenzwert | ? | |||
| 082 | limit(lambda k:besseljzero(1,k)/k,inf) | Grenzwert | ? | |||
| 083 | 1/limit(lambda x:airyai(x)*2*x**0.25*exp(2*x**1.5/3),inf,exp=True)**2 | Grenzwert | ? | |||
| 084 | 1/limit(lambda x:airybi(x)*x**0.25*exp(-2*x**1.5/3),inf,exp=True)**2 | Grenzwert | ? | |||
| 085 | nprod(lambda k:(2*k)**2/((2*k-1)*(2*k+1)),[1,inf])*2 | Product[(2 k)^2/((2*k - 1)*(2*k + 1)), {k, 1, Infinity}]*2 | Produkt: | ? | John Wallis | 1655 |
| 086 | nprod(lambda k:(4*k**2)/(4*k**2-1),[1,inf])*2 | Produkt: | ? | |||
| 087 | sqrt(6*ln(nprod(lambda k:exp(1/k**2),[1,inf]))) | Produkt: | ? | |||
| 088 | s=lambda k: sqrt(0.5+s(k-1)/2) if k else 0;print( 2/nprod(s, [1,inf])) | Produkt: | ? | |||
| 089 | s=lambda k: sqrt(2+s(k-1)) if k else 0;print( limit(lambda k: sqrt(2-s(k))*2**(k+1), inf)) | Grenzwert | ? | |||
| 090 | 2/struveh(-1,0) | Grenzwert | ? | |||
| 091 | 2/struvel(-1,0) | Höhere Funkt.: | ? | |||
| 092 | 2/angerj(0.5,0) | Höhere Funkt.: | ? | |||
| 093 | 2/webere(0.5,0) | Höhere Funkt.: | ? | |||
| 094 | gamma(fdiv(2,3))*power(3,fdiv(2,3))/airybi(-inf,-2)/2 | Höhere Funkt.: | ? | |||
| 095 | asin(1)*2 | Höhere Funkt.: | ? | |||
| 096 | (lommels1(0.125,0.125,mpf(0.75))/(gamma(0.125+0.5)*power(2,0.125-1)*struveh(0.125,mpf(0.75))))**2 | Höhere Funkt.: | ? | |||
| 097 | (lommels2(0.125,0.125,mpf(0.75))/((struveh(0.125,mpf(0.75))-bessely(0.125,mpf(0.75)))*power(2,0.125-1)*gamma(0.125+0.5)))**2 | Höhere Funkt.: | ? | |||
| 098 | (cbrt(agm(1,sqrt(2+sqrt(3))/2))/(diff(scorergi,0) *power(3,'3/4')*power(2,'4/9')))** fdiv(3,2) | (AGM[1,Sqrt[2+Sqrt[3]]/2]^(1/3)/(2^(4/9)*3^(3/4)*ScorerGi'[0]))^(3/2) | Höhere Funkt.: | ? | ||
| 099 | gamma('1/3')/(3**fdiv(2,3)*2*scorergi(0)) | Gamma[1/3]/(3^(2/3)*2*ScorerGi[0]) | Höhere Funkt.: | ? | ||
| 100 | gamma('1/3')/(3**fdiv(2,3)*scorerhi(0)) | Gamma[1/3]/(3^(2/3)*ScorerHi[0])100 | Höhere Funkt.: | ? | ||
| 101 | b=fdiv(-1,1024);print(fdiv(22,7)-fdiv(hyper([1,5/4,3/2,7/4,2],[17/8,19/8,21/8,23/8] ,b) *165+hyper([5/4,3/2,7/4,2,2],[17/8,19/8,21/8,23/8],b) *902 +hyper([5/4,3/2,7/4,2,2,2], [1,17/8,19/8,21/8,23/8],b) *1533 +hyper([5/4,3/2,7/4,2,2,2,2], [1,1,17/8,19/8,21/8,23/8 ],b) *820,2702700) | Hypergeom. Funk. 5F4, 7F6 | ? | |||
| 102 | im(asech(-1)) | Trigonom.: asech | ? | |||
| 103 | chop(asech(2)*3/j) | Trigonom.: asech | ? | |||
| 104 | chop(asech(sqrt(2))*4/j) | Trigonom.: | ? | |||
| 105 | im(asech(inf))*2 | Trigonom.: | ? | |||
| 106 | im(atanh(j))*4 | Trigonom.: | ? | |||
| 107 | im(atanh(sqrt(3)*j))*3 | Trigonom.: | ? | |||
| 108 | im(acsch(-j))*2 | Trigonom.: | ? | |||
| 109 | im(acsch(-2*j/sqrt(3)))*3 | Trigonom.: | ? | |||
| 110 | im(acsch(-j*sqrt(2)))*4 | Trigonom.: | ? | |||
| 111 | im(acsch(-j*2))*6 | Trigonom.: | ? | |||
| 112 | acsc(1)*2 | Trigonom.: | ? | |||
| 113 | acsc(2/sqrt(3))*3 | Trigonom.: | ? | |||
| 114 | acsc(sqrt(2))*4 | Trigonom.: | ? | |||
| 115 | asec(-1) | Trigonom.: | ? | |||
| 116 | asec(sqrt(2))*4 | Trigonom.: | ? | |||
| 117 | acos(-1) | Trigonom.: | ? | |||
| 118 | acos((1+sqrt(5))/4)*5 | ArcCos[(1 + Sqrt[5])/4] 5 | Trigonom.: | ? | ||
| 119 | acos((1+e**(log(5)/2))/4)*5 | ArcCos[(1 + E^(Log[5]/2))/4] 5 | Trigonom.: acos | ? | ||
| 120 | acos(0.5)*3 | Trigonom.: | ? | |||
| 121 | asin(0.5)*6 | Trigonom.: | ? | |||
| 122 | asin(sqrt(5)/4-0.25)*10 | Trigonom.: | ? | |||
| 123 | asin((1+sqrt(5))/4)*10/3 | Trigonom.: | ? | |||
| 124 | asin((1+e**(log(5)/2))/4)*10/3 | Trigonom.: | ? | |||
| 125 | acot(1))*4 | Trigonom.: | ? | |||
| 126 | atan(fdiv(1,sqrt(3)))*6 | Trigonom.: | ? | |||
| 127 | acot(5)*16-4*acot(239) | ArcCot[5]*16-4*ArcCot[239] | Trigonom.: Machin-like | ? | John Machin | 1706 |
| 128 | (atan(mp.fdiv(1,2))+mp.atan(mp.fdiv(1,3)))*4 | Trigonom.: Machin-like | ? | Euler | 1737 | |
| 129 | acot(57)*176+acot(239)*28-acot(682)*48+acot(12943)*96 | Trigonom.: Machin-like | ? | F. C. M. St⌀rmer | 1896 | |
| 130 | acot(172)*352+204*acot(239)+128*acot(682)+176*acot(5357)+272*acot(12943) | Trigonom.: Machin-like | ? | |||
| 131 | acot(2852)*6348+1180*acot(4193)+2372*acot(4246) +1436*acot(39307) +1924 *acot(55603) +2500*acot(211050) -2832*acot(390112) | Trigonom.: Machin-like | ? | |||
| 132 | appellf1(-0.5,0.5,0.01,1.5,1,0)*4 | AppellF1[-1/2,1/2,1/100,3/2,1,0]*4 | Hypergeom. Funk. F1 | ? | ||
| 133 | appellf1(0.5,0.5,0.5,1.5,1,0)*2 | AppellF1[1/2,1/2,1/2,3/2,1,0]*2 | Hypergeom. Funk. F1 | ? | ||
| 134 | appellf1(-0.5,0.5,0.5,1.5,1,0)*4 | AppellF1[-1/2,1/2,1/2,3/2,1,0]*4 | Hypergeom. Funk. F1 | ? | ||
| 135 | appellf1(0.5,0.5,0.5,1.5,0.5,0)*mp.sqrt(8) | AppellF1[1/2,1/2,1/2,3/2,1/2,0]*Sqrt[8] | Hypergeom. Funk. F1 | ? | ||
| 136 | sqrt(3)*12-12-6*appellf2(0.5,-0.5,1,0.5,2,0.25,0.5) | Sqrt[3]*12-12-6*AppellF2[1/2,-1/2,1,1/2,2,1/4,1/2] | Hypergeom. Funk. F1 | ? | ||
| 137 | sqrt((log(fdiv(19999,10000))**2/2+polylog(2,fdiv(10000,19999))-(-fdiv(1,10000))**2/4*appellf3(1,1,1,1,3,fdiv(1,10000),fdiv(1,10000)))*12) | Sqrt[(Log[19999/10000]^2/2+PolyLog[2,10000/19999]- 2.5*^-9 *AppellF3[1,1,1,1,3,1*^-4,1*^-4])*12] | Hypergeom. Funk. F3, PolyLog | ? | ||
| 138 | (51885171624116224000*sqrt(10005))/(1651969144908540723200 *hyp3f2(fdiv(1,6),0.5, fdiv(5,6),1,1,fdiv(-1,151931373056000)) -30285563*hyp3f2(fdiv(7,6),1.5, fdiv(11,6),2,2, fdiv(-1,151931373056000))) | (51885171624116224000 Sqrt[10005])/(1651969144908540723200 HypergeometricPFQ[ {1/6,1/2,5/6}, {1,1}, -(1/151931373056000)]-30285563 HypergeometricPFQ[ {7/6,3/2,11/6},{2,2}, -(1/151931373056000)]) | Hypergeom. Funk. 3F2 | ? | Gregory Chudnovsky | 1988 |
| 139 | rf(1,0.5)**2*4 | Pochhammer[1, 1/2]^2*4 | Höhere Funkt.: Pochhammer | ? | ||
| 140 | (rf(1,1.5)*4/3)**2 | Höhere Funkt.: Pochhammer | ? | |||
| 141 | (rf(1,2.5)*8/15)**2 | Höhere Funkt.: Pochhammer | ? | |||
| 142 | 4/binomial(1,0.5) | 4/Binomial[1, 1/2] | Höhere Funkt.: Binomial reell | ? | Binomial[n, k] = Gamma[n + 1]/(Gamma[k + 1] *Gamma[n - k + 1]) | |
| 143 | (zeta(4)*90)**0.25 | Höhere Funkt.: Zeta | ? | |||
| 144 | (zeta(10)*93555)**fdiv(1,10) | Höhere Funkt.: Zeta | ? | |||
| 145 | (fac(0.5)*2)**2 | Höhere Funkt.: | ? | |||
| 146 | ellipk(0)*2 | Höhere Funkt.: | ? | |||
| 147 | ellipk(0.1)*2/hyp2f1(0.5,0.5,1,0.1) | Höhere Funkt.: | ? | |||
| 148 | ellipe(0.1)*2/hyp2f1(-0.5,0.5,1,0.1) | Höhere Funkt.: | ? | |||
| 149 | ellipe(0)*2 | Höhere Funkt.: | ? | |||
| 150 | (besselk(1.5,1)*e)**2/2 | Höhere Funkt.: | ? | |||
| 151 | besselk(fdiv(1,3),fdiv(2,3))/airyai(1)/sqrt(3) | Höhere Funkt.: | ? | |||
| 152 | 2/(besseli(1.5,1)*e)**2 | Höhere Funkt.: | ? | |||
| 153 | 1/(bessely(0,2)*besselj(1,2)-bessely(1,2)*besselj(0,2)) | Höhere Funkt.: | ? | |||
| 154 | (sin(1)/besselj(0.5,1))**2*2 | Höhere Funkt.: | ? | |||
| 155 | ((hyp1f1(-0.5,0.5,-1)-1/e)/erf(1))**2 | Hypergeom. Funk. 1F1 | ? | |||
| 156 | hyp2f1(1,1,1.5,0.5)*2 | Hypergeom. Funk. 2F1 | ? | |||
| 157 | hyp2f1(0.5,1,1.5,-1)*4 | Hypergeom. Funk. 2F1 | ? | |||
| 158 | (hyp2f1(fdiv(1,3),1,fdiv(7,3),-1)*27/4+9-log(64))/2/sqrt(3) | Hypergeom. Funk. 2F1 | ? | |||
| 159 | 4*hyp2f1(1,0.25,fdiv(5,4),-0.25)+2*acot(2)-log(5) | Hypergeom. Funk. 2F1 | ? | |||
| 160 | (hyp2f2(0.5,0.5,0.5,1.5,-1)*2/erf(1))**2 | Hypergeom. Funk. 2F2 | ? | |||
| 161 | -chop(log(-1)*j) | Elementare Funktion komplex | ? | |||
| 162 | im(log(-1)) | Elementare Funktion komplex | ? | |||
| 163 | arg(-1) | Elementare Funktion komplex | ? | |||
| 164 | 2/jacobi(0.5,-0.5,0.5,1) | 2/JacobiP[1/2, -1/2, 1/2, 1] | Höhere Funkt.: | ? | ||
| 165 | 16/sqrt(27)/jacobi(0.5, 0.5, 0.5, 0.5) | 16/Sqrt[27]/JacobiP[1/2, 1/2, 1/2, 1/2] | Höhere Funkt.: | ? | ||
| 166 | sqrt('2/5')/jacobi(0.5, -0.5, 0.5, '1/4') | Sqrt[2/5]/JacobiP[1/2, -1/2, 1/2, 1/4] | Höhere Funkt.: | ? | ||
| 167 | digamma(3/4)-digamma(1/4) | Höhere Funkt.: | ? | |||
| 168 | chop(polylog(1,2)*j) | Höhere Funkt.: PolyLog | ? | |||
| 169 | -im(polylog(1,3)) | Höhere Funkt.: PolyLog | ? | |||
| 170 | si(inf)*2 | Höhere Funkt.: | ? | |||
| 171 | chop(ci(-inf)/j) | CosIntegral[-Infinity]/I | Höhere Funkt.: | ? | ||
| 172 | chop(limit(lambda k: shi(j*k)/j,inf))*2 | SinhIntegral[I Infinity]*2/I | Grenzwert | ? | ||
| 173 | chop(limit(lambda k: chi(j*k)/j,inf))*2 | CoshIntegral[I Infinity]*2/I | Grenzwert | ? | ||
| 174 | nsum(lambda k: (-1)**(k)*fibonacci(2*k+1)/((2*k+1)*phi**(4*k+2)),[0,inf])*sqrt(80) | Sum[(-1)^(k)*Fibonacci[2*k + 1]/((2*k + 1)*GoldenRatio^(4*k + 2)), {k,0, Infinity}]*Sqrt[80] | Reihe: Fibonacci | ? | phi=(1+sqrt(5))/2 | |
| 175 | nsum(lambda k: atan(1/fibonacci(2*k+1)),[1,inf])*4 | Sum[ArcTan[1/Fibonacci[2*k + 1]], {k, Infinity}]*4 | Reihe: Fibonacci | ? | ||
| 176 | nsum(lambda k: 1/((k+1)*binomial(2*k+2,k+1)),[0,inf])*3*sqrt(3) | Reihe: Binomial | ? | |||
| 177 | (nsum(lambda k: 1/((k**4)*binomial(2*k,k)),[1,inf])*3240/17)**0.25 | Reihe: | ? | Louis Comtet | 1974 | |
| 178 | (nsum(lambda k: 3*(3125347237*k**4-885673181*k**5-2942969225*k**3+1031962795*k**2-196882274*k+10996648)/((2**(k-1))*binomial(7*k,2*k)),[1,inf])-20379280)/740025 | Reihe: | ? | Fabrice Bellard | 1997 | |
| 179 | nsum(lambda n: (-1)**n/2**(10*n)*(-32/(4*n+1)-1/(4*n+3)+256/(10*n+1)-64/(10*n+3)-4/(10*n+5)-4/(10*n+7)+1/(10*n+9)),[0,inf])/64 | Sum[(2^8/(1+10 k)-2^6/(3+10 k)-2^5/(1+4 k)-4/(5+10 k)-4/(7+10 k)+1/(9+10 k)-1/(3+4 k))*(-1)^k/2^(10 k+6), {k, 0, Infinity}] | Reihe: BBP 2^10=1024 | ? | Fabrice Bellard | 1997 |
| 180 | sqrt(10005)*426880/(nsum(lambda n: fac(6*n)*(13591409+n*545140134)/(fac(3*n)*fac(n)**3*(-640320)**(3*n)),[0,inf])) | Sqrt[10005]*426880/Sum[(6*n)!*(13591409+n*545140134)/((3*n)!*n!^3*( -640320)^(3*n)), {n,0,Infinity}] | Reihe: Kehrwert | 2 | Gregory Chudnovsky  | 1988 |
| 181 | sqrt((nsum(lambda n: 2**(n+1)*fac(n)**2/fac(2*n+2),[1,inf])+1)*8) | Reihe: | ? | Oyama Shokei & Yamaji Nushizumi | 1765 | |
| 182 | (nsum(lambda n: 1/((2*n+1)**2+n),[0,inf])-log(2))*6 | Sum[1/((2*n + 1)^2 + n), {n, 0, Infinity}]*6 - Log[2]*6 | Reihe: Log[2] | ? | ||
| 183 | limit(lambda n:(fac2(2*n))**2/(n*(fac2(2*n-1))**2),inf) | Grenzwert | ? | |||
| 184 | limit(lambda n:fac(n)**2*exp(2*n)/(n**(2*n+1)*2),inf) | Limit[(n!)^2*Exp[2*n]/n^(2*n + 1)/2, n -> Infinity] | Grenzwert | ? | Stirling's asymptotic formula for n! | |
| 185 | limit(lambda n:4*16**n*n*fac(n)**4/(fac(2*n+1))**2,inf) | Limit[4*16^n*n*n!^4/(2*n + 1)!^2, n -> Infinity] | Grenzwert | ? | gamma(1/2) | |
| 186 | limit(lambda k: kei(0,k),0)*(-4) | KelvinKei[0, 0]*(-4) | Grenzwert | 999 | langsam & ungenau oder Funktionsdef. | |
| 187 | findroot(lambda x:(gamma(0.75)*jtheta(3,0,exp(-x)))**4-x,3.14) | Grenzwert | ? | |||
| 188 | re(findroot(lambda x:2*nprod(lambda k: sec(x/2**k), [2,inf])-x,3.14, solver='muller')) | Nullstellensuche: | ? | |||
| 189 | findroot(lambda x:3*sqrt(2)*cosh(x*sqrt(3)/2)**2*csch(x*sqrt(2))/nprod(lambda k: (1+1/k+1/k**2)**2/(1+2/k+3/k**2),[1,inf])-x,3.14) | Nullstellensuche: | ? | |||
| 190 | 1/log(limit(lambda n: nprod(lambda k: acsc(1)/(atan(k)),[n,2*n]), inf),4) | Grenzwert | ? | |||
| 191 | findroot(lambda x:nsum(lambda k: 72/(k*expm1(k*x))-96/(k*expm1(2*x*k)) +24/(k*expm1(4*x*k)),[1,inf])-x,3.14) | Nullstellensuche: | ? | |||
| 192 | acot(577)*1288+304*acot(682)+556*acot(1393) +624*acot(12943) +528*acot(32807) +176*acot(1049433) | Trigonom.: Machin-like | ? | |||
| 193 | (acot(40515)*19162+12000*acot(51412)+9000*acot(219602)+11407*acot(734557) +26463*acot(1039784) -6271*acot(6826318) -2988*acot(7626068) -15764*acot(9639557) +183*acot(21072618) +8419*acot(2539791558))*4 | (19162*ArcCot[40515]+12000*ArcCot[51412]+9000*ArcCot[219602] +11407*ArcCot[734557] +26463*ArcCot[1039784] -6271*ArcCot[6826318] -2988*ArcCot[7626068] -15764*ArcCot[9639557] +183*ArcCot[21072618] +8419*ArcCot[2539791558])*4 | Trigonom.: Machin-like | ? | ||
| 194 | chop(log((1+j)/(1-j))*2/j) | Elementare Funktion komplex | ? | |||
| 195 | nsum(lambda n: 1/binomial(8*n,4*n)/9**n*(5717/(8*n+1)-413/(8*n +3)- 45/(8*n+5)+5/(8*n+7)),[0,inf])/1024/sqrt(3) | Sum[(1/Binomial[8 n, 4 n]/9^n)*(5717/(8*n+1)-413/(8*n+3)- 45/(8*n+5)+5/(8*n+7)),{n,0,Infinity}]/1024/Sqrt[3] | Reihe: Binom,Pow | 022 | Cetin Hakimoglu-Brown | 2009 |
| 196 | (gamma('3/4')/(legendre(0.5,0)*gamma('5/4')))**2/2 | (Gamma[3/4]/(LegendreP[1/2,0]*Gamma[5/4]))^2/2 | Höhere Funkt.: LegendreP | ? | ||
| 197 | sqrt(lerchphi(1,2,1)*6) | Sqrt[LerchPhi[1,2,1]*6] | Höhere Funkt.: LerchPhi | ? | ||
| 198 | acos(chebyt(-1,-1)) | ArcCos[ChebyshevT[-1,-1]] | Trigonom.: acos, ChebyshevT | ? | ||
| 199 | sqrt(12*lerchphi(-1,2,1)) | Sqrt[12*LerchPhi[-1,2,1]] | Höhere Funkt.: LerchPhi | ? | ||
| 200 | (-legenq(0.5,0,0)*gamma(0.25)**2/2)**fdiv(2,3) | (-LegendreQ[1/2,0]*Gamma[1/4]^2/2)^(2/3) | Höhere Funkt.: LegendreQ | ? | ||
| 201 | (expint(0.5,1)/(1-erf(1)))**2 | (ExpIntegralE[1/2,1]/(1-Erf[1]))^2 | Höhere Funkt.: ExpIntegralE, erf | ? | ||
| 202 | (expint(0.5,1)/(erfc(1)))**2 | Höhere Funkt.: ExpIntegralE, erfc | ? | |||
| 203 | (fac2(0.5)*2*gamma(0.75))**fdiv(4,3) | (Factorial2[1/2]*2*Gamma[3/4])^(4/3) | Höhere Funkt.: | ? | ||
| 204 | chop((gamma(0.25)/(eta(j)*2))**fdiv(4,3)) | (Gamma[1/4]/(DedekindEta[I]*2))^(4/3) | Höhere Funkt.: | ? | ||
| 205 | (gamma(0.25)**2/(ellipf(asin(1),-1)*4))**2/2 | (Gamma[1/4]^2/(EllipticF[ArcSin[1],-1]*4))^2/2 | Höhere Funkt.: | ? | ||
| 206 | gamma(0.25)**4/(ellipk(-1)**2*32) | Gamma[1/4]^4/(32*EllipticK[-1]^2) | Höhere Funkt.: | ? | ||
| 207 | ellippi(-3,0)*4 | EllipticPi[-3,0]*4 | Höhere Funkt.: | ? | ||
| 208 | elliprf(0,1,1)*2 | Integrate[1/(Sqrt[(t+0)*(t+1)*(t+1)]),{t,0,Infinity}] | Höhere Funkt.: | ? | ||
| 209 | elliprc(0,1)*2 | ArcCos[Sqrt[0]/Sqrt[1]]*2/(Sqrt[1-0/1]*Sqrt[1] | Höhere Funkt.: elliprc | ? | elliprc Doku | |
| 210 | elliprj(0,1,1,2)*(4+sqrt(8))/3 | Höhere Funkt.: | ? | |||
| 211 | 2/(jtheta(3,0,0)/sqrt(ellipk(0)))**2 | 2/(EllipticTheta[3,0,0]/Sqrt[EllipticK[0]])^2 | Höhere Funkt.: | ? | ||
| 212 | (ff(0.5,0.5)*2)**2 | ((Gamma[3/2]/Gamma[1])*2)^2 | Höhere Funkt.: | ? | Fallende Faktorielle | |
| 213 | betainc(0.5,0.5,0,1) | Höhere Funkt.: | ? | |||
| 214 | (hyperfac(-0.5)/(2**fdiv(1,12)*exp((euler-zeta(2, derivative=1)/ zeta(2)-1)/8)))**8 | (Hyperfactorial[-1/2]/2^(1/12)/Exp[(EulerGamma -Zeta'[2]/ Zeta[2]-1)/8])^8 | Höhere Funkt.: | ? | ||
| 215 | -re(siegeltheta(j))*2 | -Re[siegeltheta[I/1]]*2 | Höhere Funkt.: | ? | ||
| 216 | siegeltheta(1234.55)/(nzeros(1234.55)-1-backlunds(1234.55)) | Höhere Funkt.: | ? | |||
| 217 | sqrt((apery+log(2)**3*4/21-polylog(3,0.5)*8/7)*21/(log(2)*2)) | Sqrt[(Zeta[3]+Log[2]^3*4/21-PolyLog[3,1/2]*8/7)*21/(Log[2]*2)] | Höhere Funkt.: PolyLog | ? | ||
| 218 | appellf3(1,0.01,1,9,1.5,0.5,0)*2 | AppellF3[1,1/100,1,9,3/2,1/2,0]*2 | Hypergeom. Funk. F3 | ? | Hypergeometric2F1[1,1,3/2,1/2]*2 | |
| 219 | appellf4(1,1,1.5,9,0.5,0)*2 | AppellF4[1,1,3/2,9,1/2,0]*2 | Hypergeom. Funk. F4 | ? | Hypergeometric2F1[1,1,3/2,1/2]*2 | |
| 220 | ellipk(0.5)*2/appellf4(0.5,0.5,9,1,0,0.5) | EllipticK[1/2]*2/AppellF4[1/2,1/2,9,1,0,1/2] | Hypergeom. Funk. F4 | ? | ||
| 221 | root((gamma(1/4)**2/2/appellf4(0.5,0.5,8,1,0,0.5))**2,3) | ((Gamma[1/4]^2/2/AppellF4[1/2,1/2,8,1,0,1/2])^2)^(1/3) | Hypergeom. Funk. F4 | ? | ||
| 222 | hyp2f3(0.5,1,3/4,5/4,1.5,1/4)*4/(erf(1)*erfi(1)) | Höhere Funkt.: 2F3, erf | ? | |||
| 223 | (gamma(3/4)/(gegenbauer(0.5,0.5,0)*gamma(5/4)))**2/2 | (Gamma[3/4]/(GegenbauerC[1/2,1/2,0]*Gamma[5/4]))^2/2 | Höhere Funkt.: GegenbauerC | ? | ||
| 224 | sqrt((log(khinchin)*log(2)+log(2)**2/2-nsum(lambda k:polylog(2,1/(1-k**2)), [2,inf]))*6) | Sqrt[(Log[Khinchin]*Log[2]+Log[2]^2/2-Sum[PolyLog[2,-(1/(k^2-1))], {k,2,Infinity}])*6] | Höhere Funkt.: PolyLog | ? | ||
| 225 | (hermite(-1,0)*2)**2 | (HermiteH[-1,0]*2)^2 | Höhere Funkt.: | ? | ||
| 226 | im(log(taufrom(q=0.5)))*2 | -Log[EllipticNomeQ[1/2]] | Höhere Funkt.: | ? | ||
| 227 | re(findroot(lambdax:1.0+ellipfun('cd',x,0),fdiv(22,7),solver='muller')) | InverseJacobiCD[-1,0] | Höhere Funkt.: InverseJacobiCD | ? | Umstellung/Nullstellensuche | |
| 228 | re(findroot(lambda x: 1.0+ellipfun('cn', x,0), fdiv(1299139324288,413528890451), solver='muller')) | InverseJacobiCN[-1, 0]=InverseJacobiCN[-1, 1]/I | Höhere Funkt.: InverseJacobiCN | 055 | Umstellung/Nullstellensuche | 2025 |
| 229 | -4*re(findroot(lambda x: 1.0+ellipfun('cs', x,0), -fdiv(22,28), solver='muller')) | -InverseJacobiCS[-1, 0]*4 | Höhere Funkt.: InverseJacobiCS | 055 | Umstellung | 2025 |
| 230 | chop(((sqrt(2)*cos(1)+(1+j)*cosh(1))*j/2/bei(-0.5,(-1)**fdiv(3,4)))**2) | ((Sqrt[2] Cos[1]+(1+I) Cosh[1])*I/2/KelvinBei[-1/2,(-1)^(3/4)])^2 | Höhere Funkt.: KelvinBei | 022 | Umstellung | 2025 |
| 231 | chop(-(cos(1)-root(-1,4)*cosh(1))**2/(ber(-0.5,-(-1)**fdiv(3,4)))**2)/2 | -((Cos[1]-(-1)^(1/4) Cosh[1])^2/(2 * KelvinBer[-1/2,-(-1)^(3/4)]^2)) | Höhere Funkt.: KelvinBer | 022 | Umstellung | 2025 |
| 232 | (harmonic('7/4')+log(8)-fdiv(40,21))*2 | (HarmonicNumber[7/4] + Log[8] - 40/21)*2 | Höhere Funkt.: HarmonicNumber | 022 | Umstellung | 2025 |
| 233 | (hyp3f2(1,1,-3/4,2,2,1)*7/4+log(8)-fdiv(40,21))*2 | (HypergeometricPFQ[{1, 1, -3/4}, {2, 2}, 1]*7/4 + Log[8] - 40/21)*2 | Hypergeom. Funk. 3F2 | 999 | Umstellung | 2025 |
| 234 | (psi(0,'11/4')+log(8)+euler-fdiv(40,21))*2 | (PolyGamma[0, 11/4] + Log[8] + EulerGamma - 40/21)*2 | Höhere Funkt.: PolyGamma | 022 | Umstellung | 2025 |
| 235 | ellipk(0.5)**fdiv(2,3)*(-gamma(-0.25))**fdiv(4,3)/4 | EllipticK[1/2]^(2/3)(-Gamma[-(1/4)])^(4/3)/4 | Höhere Funkt.: | ? | ||
| 236 | chop(findroot(lambdax:csch(x)*x-fac(-j)*fac(j),3.14)) | FindRoot[x*Csch[x]-(-I)!*I!,{x,22/7}] | Nullstellensuche: Csch,Fak | ? | ||
| 237 | findroot(lambdax:csch(x)*x-nprod(lambdak:(k**2-1)/(k**2+1),[2,inf]),3.14) | FindRoot[x*Csch[x]-Product[(k^2-1)/(k^2+1),{k,2,Infinity}],{x,22/7}] | Nullstellensuche: Csch,Prod | ? | ||
| 238 | findroot(lambdax:x*sinh(x)/(cosh(sqrt(2)*x)-cos(sqrt(2)*x)) -nprod(lambdak:(k**4-1) /(k**4+1),[2,inf]),3.14) | FindRoot[(x*Sinh[x])/(-Cos[Sqrt[2]x]+Cosh[Sqrt[2]x])-Product[(k^4-1) /(k^4+1), {k,2,Infinity}], {x,22/7}] | Nullstellensuche: Sinh,Cosh,Prod | ? | ||
| 239 | findroot(lambdax:sinh(x)/x/4-nprod(lambdak:1-1/k**4,[2,inf]),3.14) | FindRoot[Sinh[x]/(4x)-Product[1-1/(k^4),{k,2,Infinity}],{x,22/7}] | Nullstellensuche: Sinh,Prod | ? | ||
| 240 | findroot(lambdax:sinh(x)/x/2-nprod(lambdak:1+1/k**2,[2,inf]),3.14) | FindRoot[Sinh[x]/(2x)-Product[1+1/(k^2),{k,2,Infinity}],{x,22/7}] | Nullstellensuche: Sinh,Prod | ? | ||
| 241 | acot(239)*732+128*acot(1023)-272*acot(5832)+48*acot(110443)-48*acot(4841182) -400*acot(6826318) | ArcCot[239]*732+128 ArcCot[1023]-272 ArcCot[5832]+48 ArcCot[110443]-48 ArcCot[4841182]-400 ArcCot[6826318] | Trigonom.: Machin-like | ? | Hwang Chien-Lih | 1997 |
| 242 | co28 = 22*acot(28);print((co28 + acot((1 + tan(co28))/(1 - tan(co28))))*4) | co28 = 22*ArcCot[28];(co28 + ArcCot[(1 + Tan[co28])/(1 - Tan[co28])])*4 | Trigonom.: Machin-like | ? | 98646395734210062276153190241239 /1744507482180328366854565127 | |
| 243 | 4/(1+ContinuedFractionK("n^2","1 + 2*n")) | 4/(1+ContinuedFractionK[n^2,1+2 n,{n,1,\[Infinity]}]) | Kettenbruch | Brouncker atan(1)*4=  | 1680 | |
| 244 | ContinuedFractionK("(2*n-1)^2","6")+3 | ContinuedFractionK[(2 n - 1)^2, 6, {n, 1, \[Infinity]}] + 3 | Kettenbruch | 998 | ||
| 245 | 4/(1+ContinuedFractionK("(2*n-1)^2","2")) | 4/(1 + ContinuedFractionK[(2 n - 1)^2, 2, {n, 1, \[Infinity]}]) | Kettenbruch | 999 | William Brouncker | 1655 |
| 246 | 2-2/(3+ContinuedFractionK[(n-(-1)^n)*((-1)^n-n-1),2+(-1)^n,{n, 1, \[Infinity}]) | Kettenbruch | Stern | 1833 | ||
| 247 | Sqrt[8*(1 + Sum[2^(n + 1)*(n!)^2/(2*n + 2)!, {n, Infinity}])] | Reihe: | Oyama Shokei and Yamaji Nushizumi | 1765 | ||
| 248 | nprod(lambda n: (4*n**3)/((4*n**3)-3*n+1),[1,inf]) | Product[(4*n^3)/((4*n^3) - 3*n + 1), {n, Infinity}] | Produkt: | |||
| 249 | Sqrt[6*(2 - Sum[1/(n*(n + 1)^2), {n, Infinity}])] | Reihe: | ||||
| 250 | Sum[(-(1/4))^n (1/(1+2 n)+2/(1+4 n)+1/(3+4 n)),{n,0,Infinity}] | Reihe: | Spigot | |||
| 251 | (ArcTan[1/2]*6+6 Hypergeometric2F1[1/4,1,5/4,-(1/4)]+Hypergeometric2F1[ 3/4, 1,7/4,-(1/4)])/3 | Hypergeom. Funk. 2F1 | Spigot | |||
| 252 | CubeRoot[Sum[(-1)^n/(2*n + 1)^3, {n, 0, Infinity}]*32] | Reihe: cbrt | beta(3) | |||
| 253 | ((Zeta[3,1/4]-Zeta[3,3/4])/2)^(1/3) | Höhere Funkt.: Zeta | beta(3) | |||
| 254 | Limit[((n*((n+1)/(n-1))^(-n/2))^(-2*n)*(n!)^2)/(2*n), n->Infinity] | Grenzwert | Stirling's asymptotic formula for n! | |||
| 255 | Limit[n (n ((1+n)/(-1+n))^(-n/2))^(-2 n) Gamma[n]^2/2, n->Infinity] | Grenzwert | Stirling's asymptotic formula for n! | |||
| 256 | Limit[16^n*(n!)^3*((n - 1)!)/((2*n)!)^2, n -> Infinity] | Grenzwert | Gamma[1/2] | |||
| 257 | Limit[Sqrt[16*256^n*n*((n + 1)!)*(n!)^7/((2*n + 1)!)^4], n -> Infinity] | Grenzwert | Gamma[1/2] | |||
| 258 | Limit[Sqrt[128*256^n*(n+1)^4*((2*n^2)+2*n+1)*(n!)^8/((2*n+2)!)^4], n -> Infinity] | Grenzwert | Gamma[1/2] | |||
| 259 | Sqrt[(Sum[1/n^2/2^(n - 1), {n, Infinity}] + Log[2]^2)*6] | Reihe: Log[2] | ||||
| 260 | FindRoot[Sqrt[6 (Log[2]^2+2 (x^2/12-Log[2]^2/2))]-x,{x,22/7}] | Nullstellensuche: Log[2] | interessant: Solve findet das nicht! | |||
| 261 | Sum[(-1)^n/3^n/(2*n + 1), {n, 0, Infinity}]/Sqrt[3]*6 | Reihe: Sqrt | Gregory & Abraham Sharp | 1699 | ||
| 262 | Sqrt[18*Sum[n!^2/(2*n + 2)!, {n, 0, Infinity}]] | Reihe: Sqrt | Matsunaga Yoshisuke | 1739 | ||
| 263 | Block[{$MaxExtraPrecision = 800},N[RSolveValue[{a[n + 1]==2^(n*2-1)-2^n*Sqrt[2^(n*2-2) - a[n]], a[0] == 1/4}, a[1000], n], 40]]*16] | Grenzwert: Iteration | Archimedes | |||
| 264 | Module[{a=1,b=N[1/Sqrt[2],genau+1],c=1/4,d,abr=10^-genau,p=1},While[Abs[a-b]>abr, d=a;a=(a+b)/2;b=Sqrt[b*d]; c-=p*(d-a)^2; p*=2];(a+b)^2/(c*4)] | Grenzwert: Iteration Ord=2 | 3 | Gauss Legendre | 1820 | |
| 265 | 4096/(21 HypergeometricPFQ[{3/2, 3/2, 3/2}, {2, 2}, 1/64]+1280 HypergeometricPFQ[{1/2, 1/2},{1}, (8 - 3 Sqrt[7])/16]^2) | Hypergeom. Funk. 3F2, 2F1 | Umformung Index 050 | |||
| 266 | (32 (64 - Sqrt[4096 - 105 EllipticK[(8 - 3 Sqrt[7])/16]^2 (h1= HypergeometricPFQ[{3/2, 3/2, 3/2},{2,2}, 1/64])]))/(21 h1) | Hypergeom. Funk. 3F2, EllipticK | Umformung Index 050 | |||
| 267 | Sqrt[1/8]/Sum[(4*k)! (1103 + 26390*k)/(k!^4*4^(4*k)*99^(4*k + 2)), {k, 0,Infinity}] | Reihe: Kehrwert | Srinivasa Ramanujan 1/Pi; vergl. 052 | 1914 | ||
| 268 | Sum[(2*n)!*(130*n + 109)/(Pochhammer[7/6, n]*Pochhammer[11/6, n]*(-1296)^n), {n, 0, Infinity}]*Sqrt[3]/60 | Reihe: | An Algorithm for the Derivation of Rapidly | |||
| 269 | Sum[((4*n)!)^2*(6*n)!*(127169/(12*n+1)-1070/(12*n+5)-131/(12*n+7)+2/(12*n+11))/(9^(n + 1) (12*n)! (2*n)!), {n, 0, Infinity}]*Sqrt[3]/7776 | Reihe: | Cetin Hakimoglu-Brown | 2009 | ||
| 270 | (14 HypergeometricPFQ[{1/4,1/2,3/4,1,1},{1/12,5/12,7/12,23/12},1/18^4]-1441 HypergeometricPFQ[{1/4,1/2,3/4,1,1},{1/12,5/12,11/12,19/12},1/18^4]-16478 HypergeometricPFQ[{1/4,1/2,3/4,1,1},{1/12,7/12,11/12,17/12},1/18^4]+9792013 HypergeometricPFQ[{1/4,1/2,3/4,1,1},{5/12,7/12,11/12,13/12},1/18^4])/(1796256 Sqrt[3]) | Hypergeom. Funk. 5F4 | 10 | Cetin Hakimoglu-Brown | 2009 | |
| 271 | (Sum[1/(y^2 (x + 1)^2), {x, 1, Infinity}, {y, 1, x}]*120)^(1/4) | Reihe: | ||||
| 272 | (exp(loggamma(7/2))*8/15)**2 | (Exp[LogGamma[7/2]]*8/15)^2 | Höhere Funkt.: LogGamma | |||
| 273 | Hypergeometric2F1[1/4,1/4,1,-(1/8)]^2 Gamma[3/4]^4 Sqrt[2] | Hypergeom. Funk. 2F1 | An Algorithm for the Derivation of Rapidly | |||
| 274 | Gamma[1/4]^(4/3) (3/2)^(1/3)/(2 Hypergeometric2F1[1/4,3/4,1,1/9]^(2/3)) | Hypergeom. Funk. 2F1 | An Algorithm for the Derivation of Rapidly | |||
| 275 | Gamma[1/3]^3*3^(1/2)*2^(2/3)/(Hypergeometric2F1[1, 2/3, 7/6, -1/8]*18) | Hypergeom. Funk. 2F1 | An Algorithm for the Derivation of Rapidly | |||
| 276 | Gamma[1/3]^3*7*Sqrt[3]/(2^(1/3)*Sum[Pochhammer[2/3,n]*Pochhammer[1/2,n]*(102*n+59)/(Pochhammer[13/12,n]*Pochhammer[19/12,n]*(-288)^n), {n,0,Infinity}]) | Reihe: Pochhammer | An Algorithm for the Derivation of Rapidly | |||
| 277 | Gamma[1/3]^3*1729 Sqrt[3]/(2^(1/3) (14573 HypergeometricPFQ[ {1/2,2/3,1},{13/12,19/12},-(1/288)]-17 HypergeometricPFQ[ {3/2,5/3,2}, {25/12,31/12}, -(1/288)])) | Hypergeom. Funk. 3F2 | An Algorithm for the Derivation of Rapidly | |||
| 278 | Gamma[1/3]^3*91*3^(3/2)/(2^(1/3)*Sum[Pochhammer[2/3,n]*Pochhammer[1/4, n]*Pochhammer[3/4, n] (8400n^2+9248n+2297)/(Pochhammer[19/18, n] Pochhammer[25/18,n] Pochhammer[31/18,n]*(-4374)^n), {n,0,Infinity}]) | Reihe: Pochhammer | An Algorithm for the Derivation of Rapidly | |||
| 279 | Gamma[1/3]^3*12059775 Sqrt[3]/(2^(1/3) (101469975 HypergeometricPFQ[{1/4,2/3,3/4,1},{19/18,25/18,31/18},-(1/4374)]-4624 HypergeometricPFQ[{5/4,5/3,7/4,2},{37/18,43/18,49/18},-(1/4374)]-4200 HypergeometricPFQ[{5/4,5/3,7/4,2,2},{1,37/18,43/18,49/18},-(1/4374)])) | Hypergeom. Funk. 4F3, 5F4 | An Algorithm for the Derivation of Rapidly | |||
| 280 | Sqrt[Product[1/(1 - 1/Prime[k]^2), {k, Infinity}]*6] | Produkt: Prime | Euler, aus Zeta[x]; 1/(1 - 1/x^2)=x^2/(x^2 - 1) | 1800 | ||
| 281 | (atan('12/5')+atan('5/12'))*2 | (ArcTan[12/5] + ArcTan[5/12])*2 | Trigonom.: atan | Pi = 2*(acos(1/x)+atan(1/sqrt(x*x-1))), abs(x)>1 | ||
| 282 | (nsum(lambda k: 1/k**26, [1,inf])*fac(26)*6/2**25/8553103)**fdiv(1,26) | (Sum[1/k^26, {k, Infinity}]*26!*6/2^25/8553103)^(1/26) | Reihe: | Euler, vergl. Pi={Zeta(2*n)*(2*n)!*…Bernoulli… | 1800 | |
| 283 | (Sum[1/k^10, {k, Infinity}]*93555)^(1/10) | Reihe: | (zeta(10)*93555)**fdiv(1,10) | |||
| 284 | (ArcCot[7]*5 + 5 ArcCot[9] + ArcCot[32] + 5 ArcTan[7] + 5 ArcTan[9] + ArcTan[32])*2/11 | Trigonom.: atan | ||||
| 285 | ArcCot[7]*10+ArcCot[9]*10 +ArcCot[32]*2 +ArcTan[ 425690695462443599642383300896 /212849742950873728390263747553]/2 | Trigonom.: Machin-like | ||||
| 286 | 3/32 Sqrt[3] Sum[(16/(1 + 6 k) + 8/(2 + 6 k) - 2/(4 + 6 k) - 1/(5 + 6 k))/64^k,{k, 0, \[Infinity]}] | Reihe: BBP 64 | ||||
| 287 | (160 Hypergeometric2F1[1/6,1,7/6,1/64]+40 Hypergeometric2F1[1/3,1,4/3,1/64]-5 Hypergeometric2F1[2/3,1,5/3,1/64]-2 Hypergeometric2F1[5/6,1,11/6,1/64]) Sqrt[3] 3/320 | Hypergeom. Funk. 2F1 | aus 286 | |||
| 288 | Sum[(768/(24*k+3)+512/(24*k+4)+128/(24*k+6)-16/(24*k+12) -16/(24 k+14)-12/(24 k+15)+2/(24 k+20) -1/(24*k+22))/4096^k, {k, 0, Infinity}]/128 | Reihe: BBP 4096 | ||||
| 289 | Sum[(2/(1 + 4 k) + 2/(2 + 4 k) + 1/(3 + 4 k))/(-4)^k, {k, 0, \[Infinity]}] | Reihe: BBP 4 | ||||
| 290 | Hypergeometric2F1[3/4,1,7/4,-(1/4)]/3+Hypergeometric2F1[1/4,1,5/4,-(1/4)]*2+ ArcCot[2]*2 | Hypergeom. Funk. 2F1, acot | aus 289 | |||
| 291 | Sum[(-1)^k/(4^k*(2 k+1)),{k,0,Infinity}]*4-1/64 Sum[(-1)^k*(32/(4 k+1)+8/(4 k+2)+1/(4 k+3))/1024^k, {k,0, Infinity}] | Reihe: BBP 4,1024 | David H. Bailey | 2006 | ||
| 292 | ArcCot[2]*8-(384 ArcCot[32]+96 Hypergeometric2F1[1/4,1,5/4,-(1/1024)] +Hypergeometric2F1[3/4,1,7/4, -(1/1024)])/192 | Hypergeom. Funk. 2F1, acot | aus 291 | 2006 | ||
| 293 | (Integrate[Log[x]/Exp[x^2],{x,0,Infinity}]*(-4)/(EulerGamma +Log[4]))^2 | Integral: | ||||
| 294 | 3-nsum(lambda k: 4*(-1)**k/((2*k+1)**3-2*k-1),[1,inf]) | 3-Sum[4*(-1)^k/((2k+1)^3-2k-1),{k,Infinity}] | Reihe: | Nilakantha | 1500 | |
| 295 | nsum(lambda k: 6/((2*k+1)*(2*k+3)*(4*k+3)*(4*k+5)),[0,inf])+3 | Sum[6/((2 k + 1) (2 k + 3) (4 k + 3) (4 k + 5)), {k, 0, Infinity}] +3 | Reihe: | Nilakantha's formula | ||
| 296 | nsum(lambda k: 24/((4*k-2)*(4*k-1)*(4*k+1)*(4*k+2)),[1,inf])+3 | Sum[24/((4 k - 2) (4 k - 1) (4 k + 1) (4 k + 2)), {k, Infinity}] + 3 | Reihe: | Nilakantha's formula | ||
| 297 | nsum(lambda n: nsum(lambda k: (-1)**k*binomial(n, k)/((2*k+2)*(2*k+3)*(2*k+4)), [1,n])*2/2**n, [1,inf]) +fdiv(19,6) | Sum[Sum[(-1)^k*Binomial[n, k]/((2k+2) (2k+3) (2k+4)),{k,n}]*2/2^n,{n, Infinity}] + 19/6 | Reihe: | Nilakantha's formula | ||
| 298 | sqrt((912+12*hyp3f2(1,1,1, 2.5,3, 0.5)-12*hyp3f2(1,1,2, 2.5,3, 0.5))/27) -fdiv(24,9) | Sqrt[(912+12 HypergeometricPFQ[{1,1,1},{5/2,3},1/2]-12 HypergeometricPFQ[ {1,1,2},{5/2,3},1/2])/27]-24/9 | Hypergeom. Funk. 3F2 | aus 297 | ||
| 299 | nsum(lambda n: (-1)**(n + 1)/binomial(2*n+2,2*n-1), [1,inf])*2/3+3 | Sum[(-1)^(n + 1)/Binomial[2 n + 2, 2 n - 1], {n, Infinity}]*2/3 + 3 | Reihe: Binomial | Nilakantha's formula | ||
| 300 | quad(lambda t: lambertw(1/(2*t**2)), [0,inf])**2 | Integrate[LambertW[1/(2 t^2)], {t, 0, Infinity}]^2 | Integral: LambertW | |||
| 301 | Sum[(i!)^2 2^(i + 1)/(2 i + 1)!, {i, 0, Infinity}] | Reihe: Fac | Gibbons Spigot Algo (Rabinowitz and Wagon) | 1995 | ||
| 302 | Module[{a = 1, g = N[1/Sqrt[2], genau + 2], k, s = 0, p = 4, dif = 1}, While[dif > 10^-genau, {a, g} = {(a + g)/2, Sqrt[a g]}; s += p (dif = a^2 - g^2); p += p]; 4 a^2/(1 - s)] | Grenzwert: Iteration Ord=2 | 3 | Almkvist Berndt: AGM | 1988 | |
| 303 | Module[{a=N[Sqrt[2],genau+2],b=0,p,w,su},p=a+2;While[(a-b) > 10^-genau,w=Sqrt[a];su=a+b; a=(1/w+w)/2; b=(b+1)*w/su; p=(a+1)*p*b/(b+1)];p] | Grenzwert: Iteration Ord=2 | 3 | |||
| 304 | Module[{a=N[1/2,genau+99],s=N[(Sqrt[5]-2)*5,genau+99],x=1,y,z,s2,h5=1}, While[(4-x) > 10^-genau,x=5/s-1; y=(x-1)^2+7; z=((Sqrt[y^2-x^3*4]+y)*x/2)^(1/5); a=(s2=s^2)*a-((s2-5)/2+Sqrt[(s2-2*s+5) s])*h5; h5 *=5; s=25/((x/z+z+1)^2*s)]; 1/a] | Grenzwert: Iteration Ord=5 | 3 | Borwein & Bailey, aber Rundungsfehler | ||
| 305 | appellf2(1.5,0.5,1,1.5,2,0.25,0.5)*3/2 | AppellF2[3/2,1/2,1,3/2,2,1/4,1/2)*3/2 | Hypergeom. Funk. F2 | |||
| 306 | (2*(3+sqrt(5))*(atan((sqrt(5)-1)/2)-atan(2-sqrt(5))))/phi**2 | (2 (3+Sqrt[5]) (ArcTan[1/2 (Sqrt[5]-1)]-ArcTan[2-Sqrt[5]]))/GoldenRatio^2 | Trigonom.: atan, GoldenRatio | |||
| 307 | 4/exp(nsum(lambda n: (-1)**(n-1)*(1/n-log((n+1)/n)),[1,inf])) | 4/Exp[Sum[(-1)^(n - 1) (1/n - Log[(n + 1)/n]), {n, Infinity}]] | Reihe: Log | |||
| 308 | limit(lambda k:fac(k)**3*fac(k+1)*2**(4*k+2)/fac(2*k+1)**2,inf) | Limit[x!^3*(x + 1)!*2^(4*x + 2)/(2 x + 1)!^2, x -> Infinity] | Grenzwert: Bruch ganze Zahlen | |||
| 309 | Module[{B = N[103919467451041/33078593856621, genau + 2], a=1},While[Abs[a] > 10^-genau, a =Sin[B];B +=a+a^3/6+a^5*3/40 +a^7*5/112]; B] | Grenzwert: Selbstkonvergenz | 33 | |||
| 310 | Sum[(4/(1 + 6 k) + 1/(3 + 6 k) + 1/(5 + 6 k))/(-8)^k, {k, 0, Infinity}]/Sqrt[2] | Reihe: BBP 8 | 111 | BBP[1, -8, 6, {4, 0, 1, 0, 1, 0}]/√2 | ||
| 311 | ArcCot[2 Sqrt[2]]*2/3+(4 Hypergeometric2F1[1/6,1,7/6,-(1/8)] +Hypergeometric2F1[5/6, 1,11/6, -(1/8)]/5)/Sqrt[2] | Hypergeom. Funk. 2F1, acot | von BBP 8 | |||
| 312 | E^(2 (Im[LogGamma[1/4 + I/2]] - RiemannSiegelTheta[1])) | Höhere Funkt.: RiemannSiegelTheta | ||||
| 313 | RiemannSiegelZ[(3 I)/2]*Sqrt[2]*6/I | Höhere Funkt.: RiemannSiegelZ | ||||
| 314 | acos('5/13')*2+atan('5/12')*2 | (ArcCos[5/13] + ArcTan[5/12]) 2 | Trigonom.: atan, acos | 2*(acos(1/x)+atan(1/sqrt(x*x-1))) | ||
| 315 | 2/(struveh(-1/2,1)/sin(1))**2 | 2/(StruveH[-(1/2), 1]/ Sin[1])^2 | Höhere Funkt.: StruveH | |||
| 316 | acot(1000)*2+atan(1000)*2 | ArcCot[10^3]*2 + ArcTan[10^3]*2 | Trigonom.: atan, acot | acot(x)+atan(x)=Pi/2, x>0 | ||
| 317 | acot(18)*48+acot(57)*32-acot(239)*20 | ArcTan[1/18] 48 + ArcTan[1/57] 32 - ArcTan[1/239] 20 | Trigonom.: Machin-like | C. F. Gauß (1777-1855) | 1850 | |
| 318 | 4/(ContinuedFractionK[(2 n+1) (2 n+3), 4, {n,0, \[Infinity]}] +3) +2 | Kettenbruch | Euler  | |||
| 319 | 2/NProduct[RSolveValue[{a[n]==Sqrt[1+a[n-1]]/Sqrt[2],a[1]==1/Sqrt[2]},a[k],n], {k,1, Infinity},Method -> "WynnEpsilon"] | Produkt: Iteration | 888 | Vieta 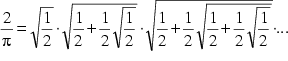 | 1593 | |
| 320 | (1/12-Sum[(2*n-2)!/((n - 1)!^2*(2*n - 3)*(2*n + 1)*2^(4*n - 2)), {n,2,Infinity}])*24 +Sqrt[3]*3/4 | Reihe: | Newton | 1666 |
